## Warning: The `size` argument of `element_rect()` is deprecated as of ggplot2 3.4.0.
## ℹ Please use the `linewidth` argument instead.

Hvorfor er det vigtigt at lære statistik?

Det er vigtigt at lære statistik fordi det er noget, der bevidst og ubevidst har stor betydning for den måde vi lever vores liv, den måde vi opfatter verden, og for den måde vi tilegner os ny viden og erfaringer, og fordi statistiske vurderinger gennemsyrer den verden vi lever i. Statistik handler helt kort om at uddrage viden fra “data”. Data, altså alle former for registreringer og målinger fra alle former for opgørelser, monitoreringer og ikke mindst videnskabelige undersøgelser og eksperimenter har i flere århundreder været en væsentlig del af det moderne menneskes gøren og laden. Ved årtusindskiftet blev anvendelsen af statistik inden for det sundhedsvidenskabelige område af førende forskere fremhævet på en 11-punktsliste over de mest vigtige bidrag til vores sundhed i 1000 år. I de seneste få år, er vi så endelig blevet ramt af den digitale tsunami, der har været under opsejling et stykke tid med computerens, internettes og kommunikationsmidlernes rivende udvikling. Man lagrer nu mængder af data i en størrelsesorden, som udvikler sig eksplosivt lige nu. Langt størstedelen af de tilgængelige data i verden i dag er genereret i løbet af de sidste 2 år, og mængden af data forventes at 10-dobles de næste 4 år! Det er tal, der næsten ikke er til at forstå, og det understreger nødvendigheden af, at vi alle bliver klædt på til en fremtid, hvor det at bruge og lære af data vil fylde mere end nogensinde, og sandsynligvis mere end nogen er i nærheden af at kunne forestille sig lige nu.

Statistikken anvender ofte sandsynligheds- og tilfældighedsbegreber for at kunne være nuanceret i forståelse af, hvad data egentlig kan og ikke kan fortælle os. Det skyldes dels, at data typisk vil være fremkommet under en vis tilfældighedspåvirkning - en patient reagerer f.eks. ikke på præcis samme måde hver gang man tager en bestemt pille, og dels at anvendelsen af den viden man vil trække ud af data kan have et tilfældighedsaspekt - f.eks. at ville forudsige en miljøpåvirkning ud i fremtiden. Derfor ses statistik og sandsynlighed ofte som to sider af samme sag - det er kun delvist rigtigt: Sandsynlighedsteorien er i sig selv en vigtig del af den matematiske teori, og har også masser af relevans for mange virkelige fænomener, som f.eks. spil og forståelsen af den grundlæggende biologi og artsudvikling. Faget statistik bruger matematik, herunder i høj grad sandsynlighedsteori, men skal som fag ses og forstås bredere end det: Det er et fag, der giver rammerne og principperne for hele processen omkring dataindsamlingen, modellering, analyse og til sidst selve vidensuddragelsen og konklusionerne, se figur senere i dokumentet. Som sådan kan man ikke konkretisere og eksemplificere statistikfagets indhold uden at gøre det i en konkret anvendelsessammenhæng. Eksempler på konkrete sammenhænge kunne være: kemi, fysik, biologi, samfundsfag, økonomi, psykologi, osv.

Data, og dermed statistik, anvendes således nu og i stigende grad på alle niveauer af vores liv: fra politiske og samfundsstyrende institutioner over al form for erhversaktivitet til helt konkrete spørgsmål på det helt personlige plan: “Kan jeg nå over vejen uden at blive kørt ned?”, “Hvem vinder det amerikanske præsentvalg? Og hvor sikre er vi på meningsmålingerne?”, “Hvor meget reduceres min risiko for svære hjerneskader ved at bruge cykelhjelm”, “Hvem vinder EM i fodbold?”, “Hvordan udvælger Facebook de reklamer, jeg ser?” “Hvordan fungerer Google translate?” Alle disse spørgsmål kan og bliver i dag forsøgt besvaret med statistik.

Statistik er desværre også et felt, hvor man let kan blive snydt af umiddelbare og øjensynligt intuitive (men alligevel forkerte) svar. Det er f.eks. velkendt at valgprognoser kun er værd at hæfte sig ved hvis interviewpersonerne er udvalgt ‘repræsentativt’. Men repræsentativt for hvad? I dansk sammenhæng er det et fornuftigt mål at gøre stikprøven repræsentativ for den samlede befolkning. Men i det engelske valgsystem med flertalsvalg i enkeltmandskredse, eller i det amerikanske system med valgmænd, kan man få helt misvisende prognoser hvis stikprøven er udvalgt uden inddragelse af disse formelle strukturer. Visse statistiske paradokser har ligefrem fået folklore-status. Det gælder f.eks. Monty Hall problemet, hvor en deltager i et tv-show skal vælge mellem tre døre, hvor der er en bil bag den ene, og Facebook Friendship paradokset, hvor de fleste mennesker på Facebook har færre venner, end deres venner har. Disse er blot pudsige eksempler på lignende problematikker af mere fundamental betydning for os alle når vi prøver at anvende sandsynlighedsbegreber og statistik til at uddrage viden. Det er med andre ord vigtigt, at man lærer at arbejde med statistik for at undgå de faldgruber, der måtte være.

Efterspørgslen på personer, der kan arbejde med statistik og dataanalyse er enorm. Behovet for personer, der er i stand til at analysere og fortolke data er vokset støt de seneste mange år, som en naturlig følge af den digitale revolution, beskrevet ovenfor. Der har næsten altid i Danmark været uddannet for få folk med disse kompetencer fra vores universiteter, og dette bliver lige nu blot værre med den voksende efterspørgsel. Der er heller ikke tvivl om at statistikkompetencerne hos alle vores højtuddannede akademikere, som ikke har statistik som deres egentlig kompetence, langt fra står mål med behovet i den moderne IT-højteknologiske verden, som de skal agere i nu og i fremtiden.

I USA har de allerede indset denne mangel på studerende med statistikkendskab og for længst startet på at få statistik ind i grundskolen og gymnasiet (rapporten med titlen SET=Statistical Education of Teachers er bestemt værd at læse).

Den 11/8 2016 skriver Berlingske om en helt ny undersøgelse, hvor Danmark halter bagefter på at klargøre vores unge mennesker til det nye digitale arbejdsmarked. Matematik og IT nævnes som nogle af de vigtige mangler. Data, statistik, og databehandling er efter vores overbevisning en central del af dette, og folkeskole og gymnasium er naturligvis fundamentet for det hele.

Når man taler statistik er det svært ikke også at tale IT. Datamængderne er ofte store, hvilket direkte nødvendiggør et CAS-værktøj til at lave de relevante beregninger, og det er ikke altid muligt at finde analytiske løsninger til de statistiske modeller. Desuden lægger den statistiske argumentationsrække direkte op til kunne formulere ved hjælp af simulationer af data-genererende processer. Fortolkningen af p-værdier, konfidensinterval, usikkerheder osv. kan alle belyses ved hjælp simulationer, hvilket blot understreger, at et CAS-værktøj fra starten bør tænkes med i hele den overordnede plan for statistikundervisningen i gymnasiet.

Statistiker og professor i digitale læringsteknologier ved DTU Compute, Helle Rootzen, har tidligere i sin egenskab af at være digital vismand skrevet en kommentar til dette i Berlingske sammen med nogle af de andre digitale vismænd. En kommentar fra Helle er: ”Overordnet kommer diskussionen af IT som fag til næsten udelukkende at handle om datalogi og kodning - som eksempel kan man tage Coding Pirates https://codingpirates.dk - som i øvrigt er et super fint initiativ. Jeg mener, at dette er helt forkert, da f.eks. statistik bør være en væsentlig del af, hvad man lærer om IT. Sagt lidt populært, hjælper det jo ikke meget at kunne kode, hvis man ikke ved, hvad man skal kode. Ofte nævner man så algoritmer, som det man skal lære, men hvordan er det så lige, at man konstruerer dem?”

Hvad er vigtigt?

I forbindelse med undervisning i statistik må det vigtigste være, at de studerende lærer nogle værktøjer, som

1. de forstår. Det er bydende nødvendigt at de studerende forstår, hvornår det giver mening at anvende eller ikke at anvende de pågældende metoder, og hvorfor de giver mening at bruge.
2. de er i stand til at anvende (så de har den nødvendige kompetence til at kunne oversætte et problem til et matematisk/statistisk problem, og kunne fortolke de resultater, der kommer ud af den matematiske model).
3. kan bruges til at analysere problemstillinger, som de støder på i dagligdagen, eller via andre fag så som fysik, biologi, samfundsfag osv (det skal være virkelighedsnært).

Det bør prioriteres højere at lære dem færre værktøjer, som de så opnår en dybere forståelse af, end at de lærer mange metoder mere overfladisk.

Som nævnt ovenfor er det svært helt at adskille statistik fra det at lære et it-værktøj. Hvis disse to ting ikke integreres vil det betyde, at gymnasieeleverne har et værktøj, som man kun sjældent kan bruge på virkelige data. Der er ingen, der orker at regne middelværdien ud af 200 observationer i hånden, eller lave en optælling og et søjlediagram af 1000 målinger. Det bør derfor tilstræbes, at de studerende har adgang til CAS-værktøjer, som kan de fornødne ting.

Statistik som en del af matematik … og andre fag

Traditionelt er statistik blevet set som del af anvendt matematik, og derfor har statistik typisk været forankret i matematikundervisningen. Denne konstruktion giver god mening fra 3 synsvinkler:

1. Sandsynlighedsregning er “ren” matematik, og sandsynlighedsberegninger indgår i statistik.
2. De logiske argumenter, der anvendes i statistikken, er af samme slags som i matematikken.
3. Matematiske modeller er ofte et vigtig element i beskrivelsen af det fænomen, som vi vil modellere.

Alle tre punkter er valide argumenter for, hvorfor statistik hører hjemme som en del af matematikundervisningen, men problemet opstår, når man glemmer, at statistik faktisk forsøger at besvare (og kvantificere) systemer, der indeholder en stokastisk komponent.

Eksempelvis har nogle af eksamensopgaverne fra gymnasiet været formuleret på nedenstående vis (løst omformuleret for at understrege pointen)

tilpas en ret linje til punkterne og find hældningen for linjen

eller

beskriv sammenhængen mellem \(x\) og \(y\) ved hjælp af en eksponentiel vækstkurve. Hvad kan du sige om væksten?

Hvis man kommer fra en matematisk baggrund giver disse opgaver god mening. Man har et problem, der skal oversættes til et matematisk problem, hvor man så kan regne løsningen ud. Der er netop en løsning på spørgsmålet, og man undersøger om den studerende er i stand til at gennemføre de tekniske trin, der er nødvendige for at løse opgaven. Man har dog helt fjernet den stokastiske komponent fra opgaverne.

Dette er helt anderledes, hvis man kommer fra andre fag, og vil belyse en eller anden sammenhæng. Her er det spørgsmål man oftest stiller noget i stil med

Her er nogle observationspunkter. Find en god model til at skrive sammenhængen.

For det første ved man jo i virkeligheden ikke, hvilken statistisk model, der er rimelig at benytte, og det er ikke engang sikkert, at der er en “korrekt” statistisk model. Man kan forestille sig en situation, hvor man eksempelvis gerne vil beskrive sammenhængen mellem børns længde/højde og deres alder. Vækstkurver har ofte form som (del af) en logistisk kurve, men hvis man kun betragter børn, som er mindre end 5 år, kan en ret linje måske ligeså vel beskrive sammenhængen (for børn under 5 år). Med andre ord kan det altså nogle gange godt være foredelagtigt at bruge en simplere model, der er god til at beskrive det konkrete fænomen vi er i gang med at modellere.

For det andet er det heller ikke muligt at give noget entydigt bud på, hvad der præcis menes med en god model. I gymnasiet har \(R^2\) i nogle fag været brugt som en slags mål for om en model var god, men det er en størrelse, der ikke nødvendigvis giver noget entydigt svar, og som ikke generelt kan bruges til at sammenligne to modeller (se andet dokument om brugen af \(R^2\)).

Denne anden type spørgsmål er måske tættere på, hvordan man i praksis ville bruge statistikken. Ulempen ved dette - i forhold til de første to spørgsmål - er, at man kan komme ud for, at to studerende besvarer det samme spørgsmål på to forskellige måder (den ene kunne fx. bruge en ret linje mens en anden brugte et 2.-grads-polynomium), og kommer frem til lidt forskellige løsninger, hvor den ene ikke er meget bedre end den anden. Dette kunne opstå, hvis den ene har tegnet data op og siger: “mit scatter plot ser ud til at jeg kan beskrive sammenhængen med en ret linje”, mens den anden siger “mit scatter plot ligner en ret linje med måske en lille krumning, så jeg bruger en parabel”. Begge personer, har i princippet argumenteret korrekt, og derfor er begge svar derfor også korrekte.

I begge situationer har de studerende vist, at de kan tænke “statistisk”, og kan oversætte en problemstilling til en matematisk relevant model, og det er denne vinkel, der mest fundamentalt adskiller statistikken fra matematikken. Hvis alle altid var enige om hvilken statistisk model, der skulle benyttes, og hvilke forudsætninger, der var gældende, så ville alle statistiske problemstillinger blive reduceret til matematiske problemer. Sådan er det desværre bare ikke, og man bliver nødt til at lære de studerende at “tænke statistisk”.

Hvordan kan man implementere statistik i gymnasieskolen?

Statistisk tankegang kan groft illustreres i nedenstående figur, hvor man har en fagspecifik virkelighed, man gerne vil beskrive. I praksis gøre det ved at formulere dette så simpelt som muligt herunder formulere de fagspecifikke spørgsmål man gerne ser besvaret, indsamle data, der kan belyse problemstillingen, og derefter oversætte denne virkelighed til en relevant statistisk model og analysemetode. Og til sidst kan man uddrage konklusioner og oversætte disse tilbage til den relevante fagspecifikke kontekst. Det er super vigtigt, at hele kæden gennemføres: målet med den statistiske analyse er at kunne udtale os om den konkrete problemstilling - ikke at løse et matematiske problem.

Figur 1: Illustration af statistisk tankegang.

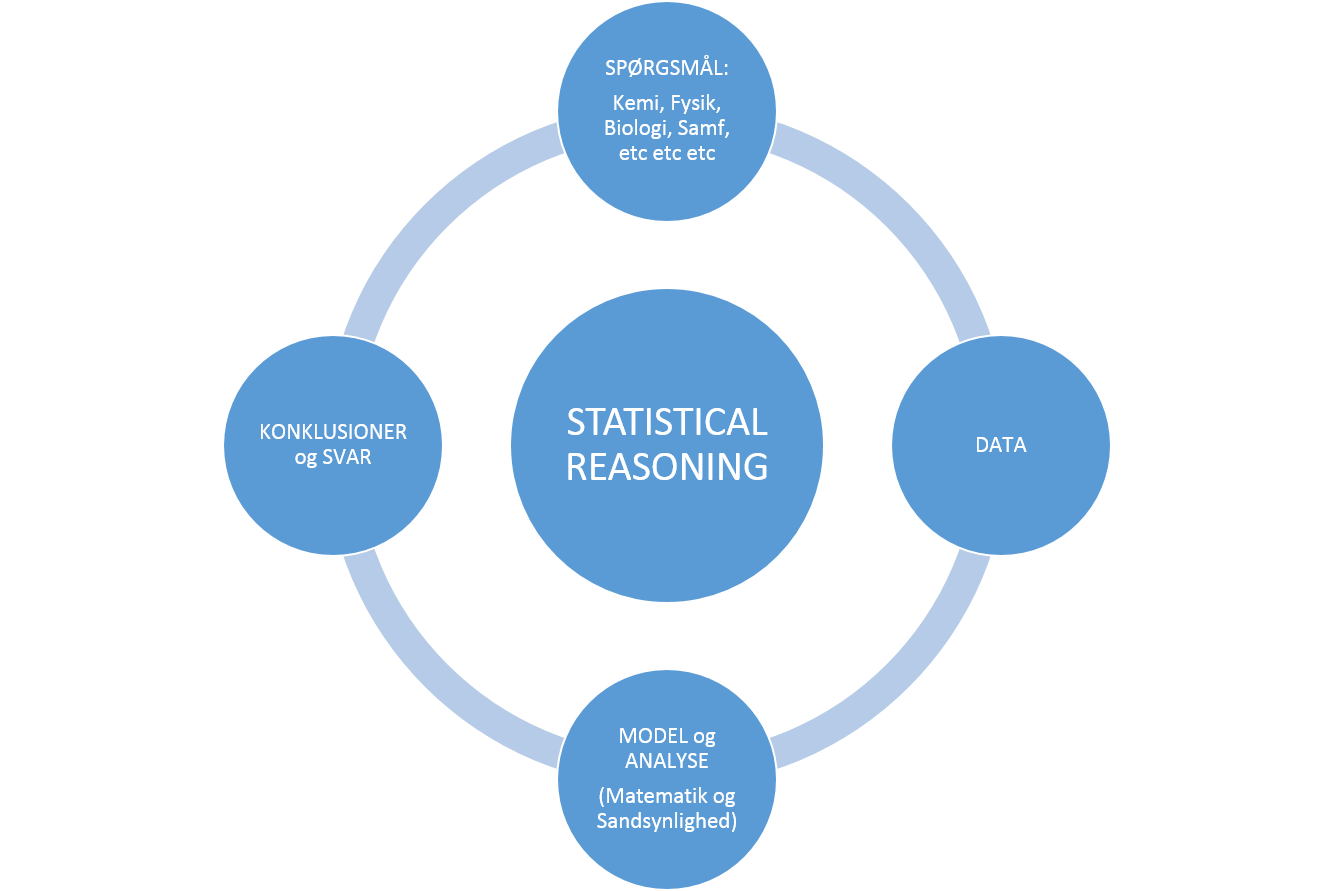
Vi ser en oplagt mulighed i at faget statistik, evt. kombineret med noget IT, kan udgøre matematiske elementer af de forskellige andre (ikke-matematiske) gymnasie-fag i en fornuftig kombination med at dele af statistikken og sandsynlighedsteorien skal være en del af selve matematikfaget. En fælles forståelse af hvad statistikken er på tværs af alle fagområderne kan så søges i f.eks. en figur a la den vist her, og de ord der skal til for at forstå den overordnede tankegang i “statistical reasoning”. De fire cirkler i figuren matcher 100% de fire punkter, som man i den amerikanske SET report anbefaler som måden man bør tænke og arbejde med statistik på high school niveau (Chapter 6, side 31-32).

En måde at integrere statistikundervisningen i matematikfaget er at bruge statistiske problemstillingen som indgang til at diskutere matematiske problemstillinger. Så sikrer man, at man ikke kun laver “matematik for matematikkens skyld”, men at man laver matematik fordi man også kan bruge det til noget.

Desuden er der jo mange ting i løbet af den daglige skolegang, der lægger op til at tale om variation. Hvis eleverne eksempelvis laver fysikrapporter er der jo ikke ualmindeligt, at de skal estimere nogle konstanter eller (tidligere) har skullet udregne \(R^2\) for en på forhånd givet model. Her kunne det være oplagt på tværs af grupperne at vise, hvor stor variation, der bare er blandt grupperne i klassen for de målte værdier.

Indtil nu har vi ikke nævnt hypotese tests direkte. Ideen bag hypotesetests er nært knyttet til den naturvidenskabelig metode og de tanker som Karl Popper præsenterede om falsificering af hypoteser i 1930’erne. Hypotesetests og \(p\)-værdier er konceptuelt ret svære, og bliver alt for ofte brugt alt for automatiseret og ukritisk. Der en generel trend i de statistikfaglige miljøer globalt set i retning af at fokusere mere på usikkerheder og konfidensintervaller end hypotesetest. The American Statistical Association (ASA) udsendte i marts 2016 for første gang i historien en pressemeddelelse med konkrete input til hvordan man (ikke) laver statistik. En meget kort version af dette kan udtrykkes som: Man kan IKKE lave statistik alene ved en eller anden automatiseret (og matematisk veldefineret) p-værdi-beregning. Verden i dag består efterhånden af alt for mange sådanne forkerte/ufuldstændige statistiske anvendelser som følge af for dårlig metodisk forståelse og indsigt globalt set. På KU Matematik berøres hypotesetest nu faktisk slet ikke i det indledende statistikkursus.

Centrale emner

• Deskriptiv statistik er vigtigt.
• Begrebet variation er vigtigt.
• Lineær regression er vigtig.
• Binomialfordelingen er vigtig.
• Chi-i-anden test er vigtig - specielt, hvis det bruges til noget mere end blot at lave hypotesetests, men at man også forsøger at beskrive relative effekter og/eller usikkerheder.
• Usikkerhedsbetragtninger er vigtigere end hypotesetest.

Overordnet set mener vi at det er udmærket at statistik-undervisningen i matematik-timerne fortsat fokuserer på to centrale problemstillinger:

1. sammenligning af binomial-sandsynligheder.
2. simpel regression, hvor observationerne modelleres ud fra én kovariat.

Men vi foreslår at begge emner åbnes op så de bruges til at italesætte bredere strømninger i den statistiske proces:

• Erfaring med data-genererende mekanismer, det vil sige simulation.
• Erfaringsbaseret forståelse af betydningsindholdet af usikkerhedsintervaller som f.eks. konfidensintervaller og prediktionsintervaller.
• Brug af deskriptiv statistik (først og fremmest tegninger) til at indkredse en relevant model, og erfaring med at forskellige data-genererende mekanismer får de deskriptive metoder til at reagere forskelligt.
• Et reelt valg mellem flere plausible modeller.

Hvis man sammenligner binomial-sandsynligheder i to grupper, skal det fremstå som lige så interessant og ønskværdigt et resultatet at binomial-sandsynlighederne er forskellige som at de er ens, og man skal kunne formulere interessante konklusioner i begge tilfælde (f.eks. konfidensintervaller for den fælles sandsynlighed i tilfælde af at grupperne er ens, separate konfidensintervaller for de to sandsynligheder i tilfælde af at grupperne er forskellige, og eventuelt et konfidensområde for oddsratio). Man skal også have en vis erfaring med trevejstabeller og med hvordan opdeling efter ekstra variable kan ændre konklusionerne.

Hvis man laver regression skal man kunne diskutere forskellige transformationer af data og eller af kovariaten. Man skal have en vis erfaring med kvadratisk regression og med regression i to grupper. Man skal kunne uddrage relevante konfidensintervaller, f.eks. for hældningen, i de forskellige tilfælde, og man skal helst også kunne sige noget om usikkerheden i forbindelse med prediktion af fremtidige observationer.

Statistik behøver ikke nødvendigvis at blive opfattet som et selvstændigt emne indenfor matematikken, da statistiske problemstillinger kan bruges som indgangsvinkel til eller udgangsvinkel på at lære nye matematiske emner. Eksempelvis lægger lineær regression direkte op til mindste kvadraters metode, simulationstankegangen og simulationer lægger op til prædiktion, integralregning/arealer kan bruges som indgang til sandsynlighedsregning, og generelle funktioner kan bruges som oplæg til modelsammenligninger.

Udfordringer

Vanskeligheden med disse udvidede diskussioner er at de ikke passer særlig godt ind i den klassiske model for matematik-undervisning.

1. En egentlig teoretisk-matematisk behandling af modellerne er for omfattende til at kunne gennemføres på gymnasialt niveau. Derfor foreslår vi at der lægges vægt på simulation og oversættelse af modelnotation til simulationer, og ikke på matematisk udledning af resultater.
2. Modsat den sædvanlige facon i matematik er der ikke ét rigtigt svar i sammenligning af modeller.
3. Det er forestår et udviklingsarbejde om hvordan man kan inddrage udvidede modelbeskrivelser i den skriftlige studentereksamen. Den ikke-matematiske natur af den undervisning vi foreslår, gør det givetvis nødvendigt at eleverne får adgang til rigtige datasæt af en anseelig størrelse ved eksamen (man skal ikke tænke i 7-8 observationer, som man typisk gør i de aktuelle regressionsopgave - man skal nærmere tænke flere hundrede observationer). Det bliver derfor vigtigt at IT-organisation af eksamen der muliggør dataadgang, og at man har optrænet en IT-parathed hos eleverne.
4. Rigtigt mange matematiklærere i gymnasiet vil have brug for en faglig opkvalificering for at kunne varetage denne type undervisning.