Kritikken af p-værdier
I september blev jeg sammen med Theis Lange bedt om at holde et diskussionsoplæg omkring den kritik, som p-værdier har været under i de seneste år. Hvorfor er kritikken opstået, hvad er problemerne, og hvad skal man mene om de alternativer, der har været foreslået til at vurdere resultaterne af videnskabelige forsøg? Emnet viste sig at være ret populært, så jeg har forsøgt at skrive dele af foredraget sammen her, da det lader til at være en problemstilling, som mange efterhånden har hørt om, og har interesse i.
Erkendelsesteori og den videnskabelige metode
P-værdier har deres udspring i erkendelsesteori, og for at forstå kritikken af p-værdierne er det værd at starte med at genopfriske erkendelsesteorien og den videnskabelige metode.
Den videnskabelige proces til at erhverve ny viden er skitseret i figuren nedenfor. Udgangspunktet er typisk en problemstilling, hypotese eller en forestilling omkring verdenen, som man ønsker at undersøge nærmere. Næste skridt er at planlægge, hvordan man vil undersøge hypotesen. Derefter indsamles data, der efterfølgende analyseres, og resultaterne sammenfattes. På dette tidspunkt er man (forhåbentlig) blevet lidt klogere på verden, og opfattelsen af problemstillingen er blevet ændret af de resultater, der er hevet ud af data. Den nye opfattelse giver anledning til nye spørgsmål/hypoteser/problemstillinger, som det er værd at undersøge i nye forsøg.
Figur 1: Den videnskabelige proces er dynamisk og dækker: 1) formulering af problemet, der ønskes belyst, 2) planlægning af forsøget og dataindsamlingen, 3) dataindsamling, -organisation og -rensning, 4) statistisk analyse og visualisering og 5) konklusion og opsummering af fund. Resultatet af processen betyder, at vi opdaterer vores viden og opfattelse af problemstillingen, hvilket giver anledning til at processen kan starte igen med afsæt i vores nye viden.
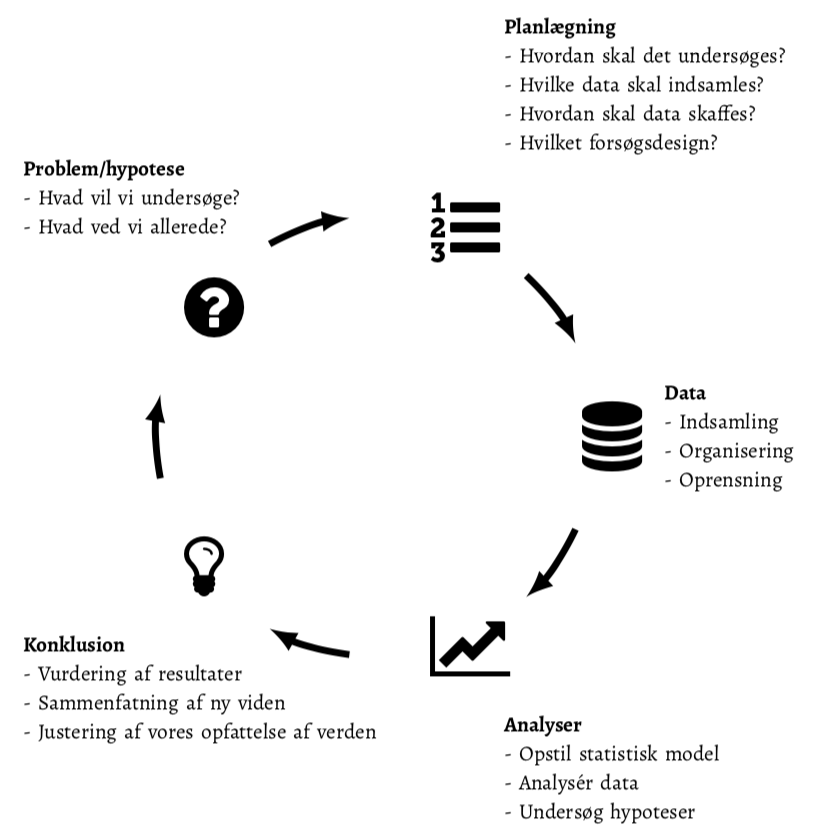
Den videnskabelige erkendelsesproces er med andre ord tænkt at være kontinuerlig og vedvarende, og som udgangspunkt forventes det ikke, at man kommer med en endelig, definitiv konklusion på baggrund af et enkelt forsøg. Først når en hypotese har vist sig at holde vand, efter at vi på bedst mulige vis har forsøgt at få den til bryde sammen, tror vi på påstanden eller hypotesen. Det er derfor, at resultaterne af et forsøg skal valideres i andre studier ved for eksempel at replicere resultaterne eller ved at sammenfatte evidensen på tværs af studier ved hjælp af metaanalyser.
Hvis den datagenererende proces, der producerer observationerne i en stikprøve, er kendt1 Sat på spidsen kunne vi sige, at hvis den datagenererende proces var kendt så behøvede vi slet ikke at undersøge noget. Så kendte vi jo allerede mekanismen, der er årsag til data i stikprøven., så betyder det, at vi kan udregne, hvor stor sandsynlighed, der er for forskellige udfald. Det er muligt at lave deduktive slutninger, fordi den datagenererende proces fuldstændig specificerer de præmisser, der måtte være for data i stikprøven, og for det system, der skal beskrives.2 Det er samme type slutninger, som benyttes indenfor matematik: hvis vi opstiller et sæt af aksiomer, hvad kan vi udlede på baggrund af logiske slutninger, som vi herefter ved gælder.
I de fleste videnskabelige forsøg benyttes imidlertid induktive slutninger eller den empirisk-induktive metode, da man netop ikke kender den datagenererende proces. Vi kan have en ide om, hvordan verden hænger sammen, men i praksis må vi tage udgangspunkt i de data vi har observeret og så se, om vi kan gætte en model, der kan tilnærme den ukendte datagenererende proces, og som kan beskrive de overordnede trends i data. Problemstillingen er vist nedenfor, og som vi skal se senere, så spiller forskellen mellem deduktive og induktive slutninger ind i debatten omkring p-værdierne.
Figur 2: Den datagenererende proces er årsag til de målinger, der observeres. Det svarer til den typiske situation indenfor matematik og sandsynlighedsregning, hvor man ud fra et sæt præmisser (den datagenererende proces) kan udtale sig om det forventede udfald. I forbindelse med de fleste videnskabelige forsøg benytter man statistisk til at gå den anden vej: vi kan se observationerne men har brug for at gætte/finde en rimelig beskrivelse af den datagenererende proces.
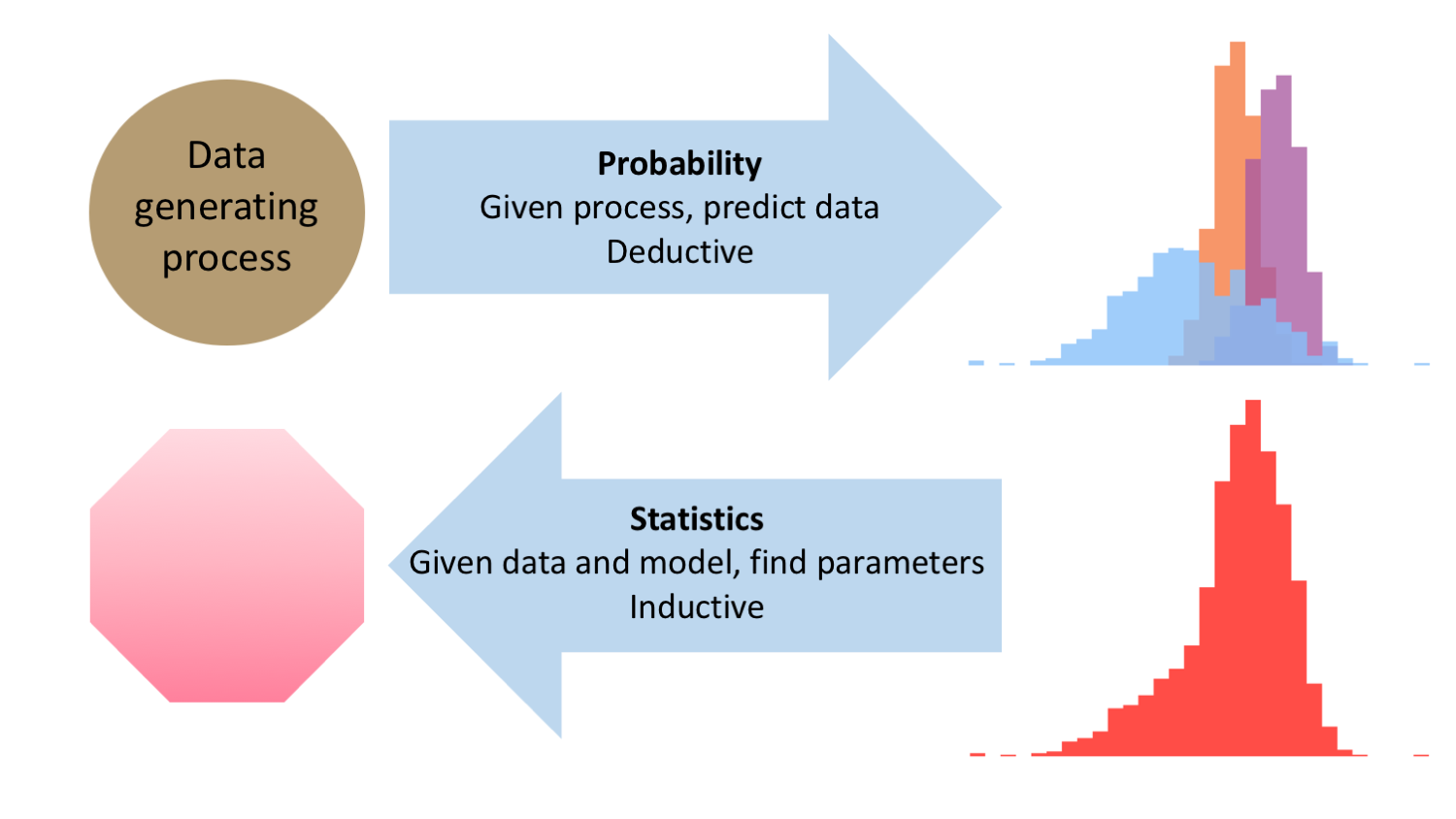
Hvad er det nu en p-værdi er?
Kirkwood og Sternes bog om Medical Statistics anvendes som undervisningsmateriale på flere studieretninger på KU SUND, og bogens formulering af en p-værdi kan man også læse i mange andre lærebøger:
The p value is the probability of having obtained a result at least as extreme as the one found with our sample if the null hypothesis were true. — Kirkwood & Sterne
En pointe, der sjældent bliver understreget i statistiklærebøger er, at når man siger “if the null hypothesis were true” så udtaler man sig ikke bare om en antagelse omkring eksempelvis en enkelt parameter, men om hele modellen, og dermed også som den forestilling om verden, som analytikeren i øvrigt gør sig. Dette kan understreges ved at pointere det i definitionen:
- Hvis nulhypotesen er sand,
- og alle andre antagelser omkring modellen også er sande,
- så er p-værdien sandsynligheden for at observere noget, der er mindst lige så ekstremt som det, du har i din stikprøve.
Med andre ord vurderer p-værdien ikke kun selve nulhypotesen, men sammenligner data med hele modellen.3 Man kan selvfølgelig argumentere for, at når man taler om “nulhypotesen”, så er det underforstået, at man mener hele modellen inklusiv restriktioner af (nogle af) parametrene, men det er ikke min opfattelse, at der er særlig mange (hvis nogen?), der tænker på nulhypotesen på denne brede måde. De fleste tænker på nulhypotesen, som restriktioner omkring en enkelt parameter. Hvis p-værdien er lille kan det derfor enten skyldes, at man har været uheldig og har observeret noget sjældent, at nulhypotesen er forkert, at modellen er forkert eller en kombination af disse.
Historikken bag p-værdierne …
I 1925 udkom Ronald Fishers bog Statistical Methods for Research Workers, hvor begrebet p-værdi blev introduceret. I bogen bruger Fisher p-værdien til at måle afvigelser mellem data og model, og han kommer med ret løse betragtninger i stil med
In preparing this table we have borne in mind that in practice we do not want to know the exact value of P for any observed \(\chi^2\), but, in the first place, whether or not the observed value is open to suspicion. If P is between .1 and .9 there is certainly no reason to suspect the hypothesis tested. If it is below .02 it is strongly indicated that the hypothesis fails to account for the whole of the facts. We shall not often be astray if we draw a conventional line at .05, and consider that higher values of \(\chi^2\) indicate a real discrepancy.
Neyman og Pearson udgav i 1928 artiklen On the use and interpretation of certain test criteria for purposes of statistical inference: part I, hvor de diskuterer brugen af p-værdier som en beslutningsregel, og hvor alternative hypoteser også introduceres. Fisher og Neyman-Pearson havde mange, årelange skænderier om hele den statistiske proces, og brugen af p-værdier uden at blive enige. Kontroverserne omkring p-værdier er altså langtfra ny.
I samme periode arbejdede Karl Popper med sit værk Logik der Forschung, der udkom i 1935.4 Og som findes her i en engelsk udgave. I bogen diskuterer Popper rammen for falsificering af videnskabelige hypoteser, og overvejelserne bag definitionen af p-værdier minder til forveksling Poppers tanker om falsificering. Poppers fokus var dog på deduktive slutninger - han var ikke den store fan af at skulle tilføje et lag af sandsynlighedsbetragtninger til hypoteserne.5 Poppers mest kendte eksempel er påstanden om at alle svaner er hvide. Her skal man bare finde en enkelt sort svane for at falsificere påstanden. Men hvad hvis ens hypotese er, at 80% af alle svaner er hvide? Så er det sværere at finde en stikprøve, der definitivt kan falsificere hypotesen. Rent logisk er det slutninger som den nedenstående, der går galt, når man går fra Poppers deduktive tankegang til en mere sandsynlighedsbaseret tankegang:
Hvis \(H\) er sand, så ser man aldrig \(D\).
Men vi har set \(D\).
Derfor må \(H\) være forkert.
bliver - når man ønsker at tilføje sandsynlighedsudsagn - (fejlagtigt) oversat til
Hvis \(H\) er sand, så ser man sandsynligvis aldrig \(D\).
Men vi har set \(D\).
Derfor må \(H\) sandsynligvis være forkert.
hvor konklusionen i sidste linje ikke holder.
I 1940 udgav Lindquist sin bog “Statistical analysis in educational research”, hvor udlægningen af brugen af p-værdier stort set svarer til den procedure, der ses i de fleste introlærebøger i statistik:
- Angiv en nulhypotese \(H_0\) og en alternativ hypotese \(H_A\). Vælg et signifikansniveau \(\alpha\) (der typisk er 5%).
- Udregn p-værdien under \(H_0\).
- Alt afhængig af p-værdien konkluderes ud fra nedenstående tabel, om nulhypotesen forkastes eller ej.
Tabel 1: De fleste lærebøger i statistik har en tabel i stil med denne omkring vurdering af resultaterne af en statistisk analyse.
| p værdi | Konklusion |
|---|---|
| \(\leq\alpha\) | Nulhypotesen forkastes, og der siges at være en signifikant effekt |
| \(>\alpha\) | Nulhypotesen forkastes ikke, og der siges ikke at være en signifikant effekt |
… og de seneste års kritik
I løbet af de seneste 15 år er kritikken af den måde, som p-værdier bruges, blusset mere og mere op. I 2005 publicerede John Ioannidis sin vigtige artikel om “Why Most Published Research Findings Are False”, hvor han blandt andet argumenterede for, at incitamentsstrukturen i den akademiske verden, og den måde, som tidsskrifter udvælger artikler til publicering, bidrager kraftigt til, at det er lettere at få publiceret statistisk signifikante resultater. Hvorvidt de videnskabelige fund senere kan valideres bliver i den sammenhæng mindre vigtig.
Denne pointe blev stærkt understreget omkring 2010, hvor det viste sig, at mange store og vigtig resultater indenfor psykologi og sociologi ikke kunne repliceres. Det blev i særdeleshed gjort klart, da en lang række forskere gav sig i kast med systematisk af replicere 100 fund fra 2008 i tre af de højest-rangerede psykologiske tidsskrifter. Den gennemsnitlige effektstørrelse i replikationsstudierne var kun halvdelen af, hvad den var i de oprindelige artikler, og blandt de 100 replikationsstudier viste kun omkring en trediedel af resultere i signifikante resultater. Det førte sin en kraftig selvransagelse indenfor disse (og andre) fag, som de stadig slikker sårene efter.
Som konsekvens af blandt andet dette besluttede editors af tidsskriftet Basic and Applied Social Psychology i 2015 sig for helt at forbyde p-værdier og konfidensintervaller. Den stigende kritik af p-værdier betød også, at the American Statistical Association i 2016 udgav et Statement on p-Values: Context, Process, and Purpose, hvor de forklarede, hvad en p-værdi er og ikke mindst, hvad den ikke er. Denne samlede udtalelse gav anledning til at flere mainstream medier også begyndte at interessere sig for problematikken.
I 2018 forslog Benjamin et al, at man skulle ændre signifikansniveauet fra 0.05 til 0.005 for at reducere risikoen for falske positiver, og her i 2019 startede Amrhein, Greenland og McShane en underskriftindsamling med mere end 800 underskrivere mod brugen af begrebet “statistisk signifikans”.6 Flere steder blev det udlagt som en kritik at p-værdier i al almindelighed, men artiklen fokuserer på problematikken omkring det at erklære noget signifikant, hvis p<0.05. Samtidig blev et helt nummer af American Statistician brugt på at diskutere, hvordan man kan få forskningsverdenen til at bevæge sig væk fra den traditionelle brug af p-værdier.
Diskussionen i de akademiske kredse har efterfølgende bredt sig til de almindelige medier, hvor fx videnskab.dk har omtalt det i flere artikler.
Hvad er så problemerne med p-værdierne?
Her er de punkter, som p-værdier ofte kritiseres for:
De svarer på det forkerte spørgsmål. En forsker er typisk interesseret i at vurdere, hvor sikker man er på den opstillede hypotese. Dette vil man gerne svare på ud fra de observerede data, så det relevante videnskabelige spørgsmål er ofte
\[P(\text{hypotesen er sand} | \text{data}).\]
P-værdien giver derimod et svar på den “omvendte sandsynlighed”7 P-værdien giver et sandsynlighedsudsagn om data ud fra en deduktiv tilgang. Den fortæller ikke noget om hypotesen.
\[P(\text{data (eller mere ekstreme data)} | \text{hypotesen er sand}).\]
Groft sagt giver p-værdien et (matematisk korrekt og nøjagtigt) svar på et spørgsmål, som man ikke er interesseret i. Her ser tydeligt forskellen mellem den induktive tankegang (det videnskabelige spørgsmål) og den deduktive tankegang, som p-værdien giver et svar på.
De indeholder flere typer information. P-værdien kombinerer og afspejler to facetter ved data: effektstørrelsen og stikprøvestørrelsen. Når effektstørrelsen eller stikprøvestørrelsen bliver større bliver p-værdien tilsvarende mindre.8 Når effekten er kraftig er det lettere at finde den, og tilsvarende gælder, at når man har store stikprøver er det lettere at finde selv små effekter. Dette kan eksempelvis ses i teststørrelsen for et almindeligt t-test, hvor man ønsker at teste, om middelværdien i en population er \(\mu_0\). Teststørrelsen er
\[T = \frac{|(\bar{X} - \mu_0)| \sqrt{N}}{s},\]
hvor \(\bar{X}\) er gennemsnittet af målingerne i stikprøven, \(s\) er stikprøvespredningen og \(N\) er stikprøvestørrelsen. Store værdier af teststørrelsen er kritiske, så når stikprøvegennemsnittet er langt fra nulhypotesen eller når \(N\) er stor, så bliver teststørrelsen automatisk stor.9 Dette viser sig at være praktisk problem i flere tilfælde, end man skulle tro. Når man arbejder med store datasæt som for eksempel udtræk fra de danske registre, så viser alle hypoteser sig at være statistisk signifikante, fordi man har så mange observationer. Konsekvensen er, at hvis man bare indsamler tilstrækkelig med data så bliver alle hypoteser signifikante.
De bliver brugt forkert. P-værdierne anvendes meget ofte som en beslutningsregel: hvis værdien er mindre end en forudbestemt signifikansgrænse (typisk 5%) siges det, at man har fundet noget “signifikant”, mens en p-værdi større end signifikansgrænsen medfører en konklusion om at der “ikke er nogen signifikant sammenhæng”. Der er flere kritikpunkter til denne fremgangsmåde.
For det første har man valgt at lave en dikotomisering af p-værdien på baggrund af en tilfældig valgt grænseværdi. P-værdien selv er udregnet på en kontinuert skala, og at to p-værdier på for eksempel 0.04 og 0.06 giver væsensforskellige konklusioner bare fordi den ene er lige over 5% og den anden er lige under 5% giver meget sjældent mening. Problemstillingen med at dikotomisere kontinuerte variable har vi allerede diskuteret tidligere, og i den videnskabelige proces er det yderst sjældent, at man skal komme med en endelig konklusion på baggrund af resultaterne fra et enkelt studie.
For det andet betyder et resultat, der er statistisk signifikant ikke, at det er biologisk relevant. Vi så ovenfor, at p-værdien også afspejler stikprøvestørrelsen, så p-værdien alene kan aldrig sige noget om, hvorvidt effekten har en relevant betydning i den virkelige verden.
Derudover ser man ofte, at studier med en p-værdi større end 0.05 konkluderer, at der ikke er nogen sammenhæng.10 Et eksempel kan ses i Effect of a Resuscitation Strategy Targeting Peripheral Perfusion Status vs Serum Lactate Levels on 28-Day Mortality Among Patients With Septic Shock, hvor overlevelsen i to grupper er på henholdsvis 43.4% og 34.9%, men forfatterne konkluderer, at “… did not reduce all-cause 28-day mortality” ud fra en p-værdi på 0.06. Det kan godt være, at forskellen i procentpoint ikke er statistisk signifikant, men en forskel på 9 procentpoint tyder på, at der godt kunne være en reel reduktion i all-cause mortality. P-værdien er udregnet ud fra antagelsen om at nulhypotesen er korrekt, og man kan derfor ikke konkludere, at man accepterer hypotesen når p-værdien er stor. Man kan vælge at forkaste eller ikke at forkaste hypotesen, men man kan ikke få nulhypotesen verificeret.
Nulhypoteserne er typisk urealistiske
Nulhypoteser er ofte formuleret ved at man sætter en parameter til en bestemt værdi, fx. \(H_0: \beta = 0\) eller at man sætter parametre for forskellige grupper lig hinanden, \(H_0 : \mu_1 = \mu_2\). Hvornår tror man egentlig på, at disse meget specifikke hypoteser korrekt angiver sammenhængen i populationen?
Hvis man eksempelvis vil undersøge, om raske mænd og kvinders blodtryk er ens, så svarer det til hypotesen
\[H_0 : \mu_\text{mænd} = \mu_\text{kvinder},\]
hvor \(\mu_\text{mænd}\) og \(\mu_\text{kvinder}\) er middelværdien i blodtryk i populationen for de to køn. Men tror vi på, at middelværdierne skal være helt identiske? Hvorfor skulle de være det - der er jo mange andre fysiologiske faktorer, der kunne resultere i små ændringer af blodtrykket, og som kunne adskille sig fra mænd og kvinder. Vi formulerer hypoteser, som lægger ret strikse antagelser ned over vores model, hvor vi i virkeligheden tænker på hypotesen som om at de to grupper er tilstrækkelig ens til at det ikke har nogen særlig betydning.
Alternative forslag til p værdier
Med alle de kritikpunkter, der har været af p-værdier er det ikke overraskende, at der er dukket forskellige forslag op til at fikse problemerne.
- Brug konfidensintervaller. Konfidensintervaller bliver ofte foreslået som alternativ til p-værdier. Konfidensintervaller har den fordel, at de ikke bare tester en enkelt hypotese, men giver et interval af værdier, hvor data ikke er i modstrid med hypotesen. Men konfidensintervaller er defineret ud fra p-værdier svarende til at man har foretaget uendelige mange tests, så hvis man synes, at p-værdier er problematiske så gør konfidensintervaller kun problemstillingen værre.
Figur 3: Et 95% konfidensinterval for en parameter μ er defineret som de værdier for μ, der ikke forkastes ved test med et signifikansniveau på 5%. Et konfidensinterval konstrueres derfor ved at lave uendelig mange hypotesetests, og registrere, hvornår hypotesen forkastes.

Et andet problem med konfidensintervaller er, at de meget ofte fortolkes forkert. Konfidensintervallet fortæller, hvilke værdier af en parameter, der resulterer i at man ikke forkaster hypotesen. Mange opfatter konfidensintervallerne anderledes, og tænker på dem, som om at værdierne midt i intervallet er mere sandsynlige end værdierne i kanten af intervallet, men det må man ikke. Metoden til at udregne et 95% konfidensinterval har den egenskab, at hvis man for eksempel udtager 100 stikprøver og for hver udregner et 95% konfidensinterval, så får man 100 forskellige konfidensintervaller, men man vil forvente at 95 af dem vil indeholde den sande parameter. Konfidensintervallet siger ikke noget om hvor i intervallet, at denne populationsparameter er mere tilbøjelig til at være. For at kunne svare på det skal man skal følge en bayesiansk tankegang og lave kredibilitetsintervaller, der netop har denne fortolkning.
Figur 4: Mange opfatter konfidensintervaller som værdier af parameteren, som man har ‘tiltro’ til, og at der er større sandsynlighed for værdierne midt i intervallet, men det siger konfidensintervallet ikke noget om. En gammel vittighed siger, at epidemiologer fejlagtigt opfatter konfidensintervaller som kredibilitetsintervaller, mens statistikere godt ved, at konfidensintervaller ikke er kredibilitetsintervaller, selvom de alligevel fortolker dem på samme måde.
Konfidensintervallerne løser derfor ikke problemerne med p-værdierne. Fra et præsentationsmæssigt synspunkt har de til gengæld den fordel, at de både angiver værdien af parameteren og den tilhørende usikkerhed, så resultatet bliver direkte sammenkoblet med den konkrete problemstilling.
Udregn bayesfaktorer i stedet. Et andet forslag til et alternativ til p-værdier er at udregne bayesfaktorer. En bayesfaktor sammenligner to hypoteser \(H_1\) og \(H_0\), og er defineret ved
\[\text{BF} = \frac{P(D|H_1)}{P(D|H_0)},\]
hvor \(P(D|H_1)\) og \(P(D|H_0)\) er sandsynligheden for data under henholdsvis \(H_1\) og \(H_0\). Hvis for eksempel \(\text{BF} = 2\) betyder det, at data er dobbelt så sandsynligt under \(H_1\) som under \(H_0\) (mere evidens for \(H_1\)). Hvis BF<1 er der mere evidens for \(H_0\). Spørgsmålet er, at hvor stor BF skal være førend at man foretrækker den ene hypotese fremfor den anden.
For at vurdere størrelsesordenen på en bayesfaktorer har flere forfattere kommet med bud på at fortolke størrelsesordenenWikipediasiden om bayesfaktorer angiver to tabeller, der begge kan bruges til at afrapportere bayesfaktorer. Den ene er gengivet nedenfor (i tabellen svarer \(K\) til bayesfaktoren).
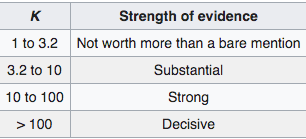
Så har man bare rykket problemet fra p-værdier til BF-værdier, men bruger stadig en tabel med inddelinger til at vurdere det endelige resultat.. Det vil sige, at bayesfaktoren rykker problemstillingen fra en skala (p-værdien er sandsynlighed for data under \(H_0\)) til en anden skala (et forhold i sandsynligheder), men når man stadig inddeler skalaen i kategorier, så giver det samme problemer, som når man inddeler p-værdien i over og under 5%.Bayesfaktoren optræder som en del af Bayes’ formel,
\[\frac{P(H_1|D)}{P(H_0|D)} = \underbrace{\frac{P(D|H_1)}{P(D|H_0)}}_\text{BF} \frac{P(H_1)}{P(H_0)},\]
hvor bayesfaktoren skalerer a priori forholdet mellem de to hypoteser. Bayesfaktoren siger altså kun indirekte noget om forholdet mellem de to hypoteser, og hvis de oprindelige sandsynligheder for de to hypoteser er meget forskellige, så er det ikke sikkert, at bayesfaktoren kan opveje dette.
Sænk signifikansgrænsen. I 2017 foreslog Benjamin og 83 andre medforfattere, at man skulle sænke signifikansgrænsen fra 0.05 til 0.005 ved test af nye fund. Argumentet for dette var, at det ville resultere i færre falsk positive fund. “Prisen” for dette vil så være, at forsøgene kræver større stikprøver for at have samme styrke som tidligere, og at man dermed nok kommer til at lave færre undersøgelser i det hele taget.
En justering af signifikansniveauet vil sænke antallet af falske positiver, hvilket naturligvis er positivt. Men det ændrer ikke ved de fundamentale problemer ved p-værdien, for det er stadig den, der ligger til grund for vurderingen, og man benytter stadig en dikotomiseret grænse til at opnå en konklusion.
Brug bayesianske metoder. Endelig foreslås det ofte, at man bruger bayesianske analysemetode som alternativ til frekventisternes p-værdier. Bayesiansk analyse har den fordel, at der svares på det spørgsmål, som forskerne typisk er interesseret i. Som bayesianer kan man nemlig knytte en sandsynlighed til selve hypotesen og udregne
\[P(H|D),\]
og kan derefter komme med udtalelser som for eksempel “jeg er 89% sikker på at parameteren er større end 0”. For at kunne dette skal man naturligvis gå ind på den bayesianske tilgang med alle de dertil hørende problemer, og denne løsning passer derfor ikke ind i en frekventistisk ramme.
Er p værdierne det store problem?
Kritikken af p-værdier er berettiget, men det er også et let mål at kritisere af den simple grund, at de er matematisk veldefinerede. For at sætte problemstillingen lidt i perspektiv, så er det værd at holde kritikken af p-værdierne op mod de mange andre aspekter af en dataanalyse.
Undervejs i en analyse foretages en lang række valg, der har enorm betydning for de resultater, man kommer frem til. For eksempel: hvilken model skal man bruge? Hvilke variable skal tages med i modellen? Hvordan skal disse variable måles? Hvilke yderligere antagelser er der omkring modellen? Hvilke variable er confoundere og hvilke er collidere? Er der collinearitet mellem de forklarende variable? Hvordan sikrer man sig mod overfitting? Hvad gør man med manglende data?
Når analysen er færdig foretages der endnu flere valg i forbindelse med præsentationen? Får man præsenteret alle de analyser, der er foretaget eller foregår der et udvalg af de bedste resultater p-hacking. Bliver studiet i det hele taget publiseret eller kommer det til at lide under, at det er sværere at publisere negative resultater?
Alle disse aspekter har enorm betydning for analysens resultater, og fordi de er sværere at beskrive, operationalisere og kvantificere bliver de også sværere at kritisere.
På trods af alle problemerne med p-værdier har de spillet en central rolle i den evidensbaserede udvikling indenfor medicin og folkesundhed i de sidste 100 år, hvor der er sket enorme fremskridt. P-værdierne har haft den effekt, at de har luget ud i de værste fejlopfattelser, og har hjulpet til med at strukturere den måde, som vi indsamler og bearbejder data på for at indsamle ny viden.
Som krølle på historien kan nævnes, at Fricker et al. i 2019 gennemgik 17 artikler, der var publiseret i Basic and Applied Social Psychology i 2016 - året efter at tidsskriftet indførte deres forbud på p-værdier - og hvor statistik blev anvendt. Fricker et al fandt flere tilfælde, hvor konklusioner i artiklerne ikke ville holde, hvis man havde brugt p-værdier og signifikanstest.
Hvad kan man gøre?
P-værdier er et af værktøjerne i statistikerens værktøjskasse, og så længe det er klart, hvad de repræsenterer, og man ikke strækker sine konklusioner længere end metoderne og data kan holde, så er p-værdier stadig nyttige.
Vigtigst er det måske nok, at p-værdierne tjener det vigtige formål, at de fungerer som en hurtig (og veldefineret) metode til at checke aspekter af data, og at de dermed forhindrer, at man laver nogle grelle fejltagelser og konklusioner.
Afrapportering af resultater bør som minimum indeholde konfidensintervaller, da de er med til at sikre, at estimatet kan forstås kontekst af den givne problemstilling.
Opfordringen om at undgå at bruge udtrykket “statistisk signifikant” (og dermed også at undgå at dikotomisere p-værdien) giver god mening, da “signifikant” af langt de fleste læsere opfattes som “relevant og vigtig”. Og det er faktisk ikke så svært at undgå at skrive det, når resultater præsenteres. Eksempelvis kan
Applying a multiple logistic regression model did not show a statistically significant difference in treatment success between treatments A and B [odds ratio (OR) = 1.22, 95% confidence interval (CI) = 0.86–1.75,P= 0.26].
omskrives til
Applying a multiple logistic regression model to examine the difference in treatment success between treatments A and B yielded an odds ratio (OR) of 1.22 [95% confidence interval (CI) = 0.86–1.75, P= 0.26].
hvor man præsenterer præcis, hvad man har fundet, og lader læseren være med til at vurdere resultaterne.
P-værdier fylder stadig meget i videnskabelig forskning, og en af grundene skyldes også den menneskelige psykologi - både blandt de videnskabelige tidsskrifter og hos dem, der laver forsøgene. Der er stor tilfredsstillelse i endegyldigt at kunne konkludere noget omkring en problemstilling, og kunne sige: “nu ved vi det”. Men for langt de fleste videnskabelige problemstillinger er det naivt at gøre sig forhåbninger om at kunne sætte to streger under et videnskabeligt fund. Derfor er det vigtigt at bruge værktøjerne - alle værktøjerne - til det, de er lavet til, og dermed bidrage til den videnskabelige proces.
The rage for wanting to conclude is one of the most deadly and most fruitless manias to befall humanity. Each religion and each philosophy has pretended to have God to itself, to measure the infinite, and to know the recipe for happiness. What arrogance and what nonsense! I see, to the contrary, that the greatest geniuses and the greatest works have never concluded. — Gustave Flaubert